TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 

 RELATIVIDADE DIMENSIONAL GRACELI.

 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Em física, a conexão de Berry e a curvatura de Berry são conceitos relacionados que podem ser vistos, respectivamente, como um potencial de gauge local e um campo de gauge associado à fase de Berry ou fase geométrica.^[1] Esses conceitos foram introduzidos por Michael Berry em um artigo publicado em 1984, enfatizando como as fases geométricas fornecem um poderoso conceito unificador em vários ramos da física clássica e quântica.^[2]

Fase de Berry e evolução adiabática cíclica

Na mecânica quântica, a fase de Berry surge em uma evolução adiabática cíclica.^[3] O teorema adiabático quântico se aplica a um sistema cujo hamiltoniano ${\displaystyle H(\mathbf {R} )}$ depende de um parâmetro (vetorial) ${\displaystyle \mathbf {R} }$ isso varia com o tempo ${\displaystyle t}$. Se o ${\displaystyle n}$'ésimo autovalor ${\displaystyle \varepsilon _{n}(\mathbf {R} )}$ permanece não degenerado em todos os lugares ao longo do caminho e a variação com o tempo t é suficientemente lento, então um sistema inicialmente no autovetor próprio normalizado ${\displaystyle \,|n(\mathbf {R} (0))\rangle }$ permanecerá em um autovalor instantâneo${\displaystyle \,|n(\mathbf {R} (t))\rangle }$ do hamiltoniano ${\displaystyle \,H(\mathbf {R} (t))}$, até uma fase, ao longo do processo. Em relação à fase, o estado no momento t pode ser escrito como^[4]

${\displaystyle |\Psi _{n}(t)\rangle =e^{i\gamma _{n}(t)}\,e^{-{i \over \hbar }\int _{0}^{t}dt'\varepsilon _{n}(\mathbf {R} (t'))}\,|n(\mathbf {R} (t))\rangle ,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde o segundo termo exponencial é o "fator de fase dinâmica". O primeiro termo exponencial é o termo geométrico, com ${\displaystyle \gamma _{n}}$ sendo a fase de Berry. Da exigência de que ${\displaystyle |\Psi _{n}(t)\rangle }$ satisfaz a equação de Schrödinger dependente do tempo, pode-se mostrar que

${\displaystyle \gamma _{n}(t)=i\int _{0}^{t}dt'\,\langle n(\mathbf {R} (t'))|{d \over dt'}|n(\mathbf {R} (t'))\rangle =i\int _{\mathbf {R} (0)}^{\mathbf {R} (t)}d\mathbf {R} \,\langle n(\mathbf {R} )|\nabla _{\mathbf {R} }|n(\mathbf {R} )\rangle ,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

indicando que a fase de Berry depende apenas do caminho no espaço de parâmetros, não da taxa em que o caminho é percorrido.

No caso de uma evolução cíclica em torno de um caminho fechado ${\displaystyle {\mathcal {C}}}$ de maneira que ${\displaystyle \mathbf {R} (T)=\mathbf {R} (0)}$, a fase de Berry de caminho fechado é

${\displaystyle \gamma _{n}=i\oint _{\mathcal {C}}d\mathbf {R} \,\langle n(\mathbf {R} )|\nabla _{\mathbf {R} }|n(\mathbf {R} )\rangle .}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Um exemplo de sistema físico em que um elétron se move ao longo de um caminho fechado é o movimento do ciclotron (detalhes são fornecidos na página da fase de Berry). A fase de baga deve ser considerada para obter a condição de quantização correta.

Proposta pelo físico estadunidense Josiah Willard Gibbs, a Regra das Fases de Gibbs apresenta um critério para a determinação das fases que coexistirão em um sistema em equilíbrio num diagrama de fase.^[1]

Índice

• 1Definição
• 2Sistema unário
• 3Sistema binário
• 4Referências
• 5Ver também

Definição

A regra das fases de Gibbs é expressa pela equação

${\displaystyle P+F=C+N}$ ,

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

em que P é o número de fases presentes, F é o número de graus de liberdade, ou o número de variáveis que podem ser controladas externamente, e que devem ser especificadas para definir por completo o estado de um sistema. O parâmetro C representa o número de componentes e N é o número de variáveis não relacionadas à composição. Como muitas vezes essas variáveis são a temperatura e a pressão, é comum a equação aparecer como:

${\displaystyle P+F=C+2}$ .

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Sistema unário

Para sistemas com um só componente, em que C = 1 e as variáveis são temperatura e pressão, de modo que N = 2, a equação toma a forma

${\displaystyle P+F=3}$ .

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

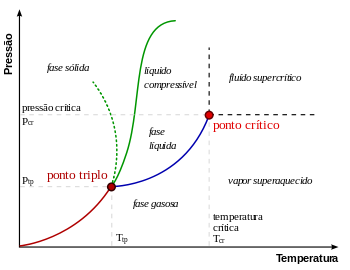
No ponto triplo coexistem três fases em equilíbrio. Como há apenas um componente, o número de graus de liberdade é dado por

${\displaystyle F=C+N-P}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle F=1+2-3}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou seja, F = 0. Isso significa que nenhuma variável (temperatura ou pressão) pode ser mudada, mantendo-se a existência das três fases.

Ao longo de um contorno de fase, duas fases estão em equilíbrio, de modo que

${\displaystyle F=1+2-2}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

e há apenas um grau de liberdade. Isso significa que para descrever o estado basta especificar apenas uma das variáveis, pois a outra já está definida.

Considerando um ponto situado em uma região com apenas uma fase,

${\displaystyle F=1+2-1}$v

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

o número de graus de liberdade nesse caso é 2. São necessárias duas variáveis para definir o estado do sistema.

Sistema binário

Para misturas binárias, há dois componentes (C = 2) e, além da temperatura e pressão, há a presença do grau de liberdade composição. Como muitas vezes as operações metalúrgicas, que fazem uso do diagrama binário, são realizadas à pressão atmosférica, a pressão é dada como constante a 1 atm, de modo que N = 1.^[2]

${\displaystyle F=C-P+1}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Denomina-se matéria degenerada, ou ainda gás degenerado, aquela na qual uma fração importante da pressão provém do princípio de exclusão de Pauli, que estabelece que dois férmions não podem ter os mesmos números quânticos.

Tal "gás" não obedece às leis clássicas segundo as quais a pressão de um gás é proporcional à sua temperatura e densidade.

Enrico Fermi e Paul Adrien Maurice Dirac provaram que, a uma densidade muito alta, a pressão aumenta rapidamente até o ponto em que ela passa a independer da temperatura do gás. Neste ponto, o gás passa a agir quase como um sólido.

Na astronomia, este gás é encontrado nas estrelas anãs brancas e é importante no tratamento tanto de estrelas residuais densas quanto das novas que as geram.^[1] É conceito importante em cosmologia e na evolução do universo no tempo,^[2] com relações com a teoria da relatividade^[3] e para o modelo "big bang" e na detecção de objetos estelares.^[4]

Dependendo das condições, a degeneração de diferentes partículas pode contribuir com a pressão de um objeto compacto, de modo que uma anã branca está sustentada pela degeneração dos elétrons, ainda que uma estrela de nêutrons não colapse devido ao efeito combinado da pressão de nêutrons degenerados e da pressão devida à ação repulsiva da interação forte entre bárions.

Estas restrições nos estados quânticos fazem com que as partículas adquiram momentos muito elevados, já que não têm outras posições do espaço de fases onde situar-se; pode-se dizer que o gás, ao não poder ocupar mais posições, se vê obrigado a estender-se no espaço de momentos com a limitação da velocidade c (velocidade da luz). Assim, ao estar tão comprimida a matéria, os estados energeticamente baixos preenchem-se em seguida, pelo que muitas partículas não têm outra possibilidade senão colocar-se em estados muito energéticos, o que envolve uma pressão adicional de origem quântica. Se a matéria está suficientemente degenerada, esta citada pressão será dominante, e muito, sobre todas as demais contribuições. Esta pressão é, além disto, independente da temperatura e unicamente dependente da densidade.

Estas características implicam tratamento termodinâmico bastante diverso e adequado às pressões e campos gravitacionais envolvidos,^[5] assim como o comportamento das reações nucleares na proximidade de tais massas.^[6][7]

Necessita-se de densidades para chegar aos estados de degeneração da matéria. Para a degeneração de elétrons se requer uma densidade em torno dos 10⁶ g/cm³, para a de nêutrons necessita-se muito mais ainda, 10¹⁴ g/cm³.

Índice

• 1Tratamento matemático da degeneração
• 2Gases degenerados
  • 2.1Degeneração de elétrons
    • 2.1.1Situação nos gases ordinários
    • 2.1.2Situação em altas densidades
    • 2.1.3O limite de Chandrasekhar
  • 2.2Degeneração de prótons
  • 2.3Degeneração de nêutrons
    • 2.3.1As estrelas de nêutrons
    • 2.3.2Comparação com o gás degenerado de elétrons
    • 2.3.3O limite de Tolman-Oppenheimer-Volkoff
  • 2.4Degeneração de quarks
• 3Tipos especulativos de matéria degenerada
  • 3.1Degeneração de préons
• 4Referências
• 5Veja também
• 6Ligações externas
  • 6.1Noções simplificadas
  • 6.2Tratamentos mais formais

Tratamento matemático da degeneração

Para calcular o número de partículas fermiônicas em função de seu momento, se usará a distribuição de Fermi-Dirac (ver estatística de Fermi-Dirac) da seguinte maneira:

${\displaystyle n(p)dp=2\cdot {\frac {4\pi p^{2}dp}{h^{3}}}\cdot {\frac {1}{1+exp\left({\frac {E_{p}}{KT}}-\psi \right)}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Onde n(p) é o número de partículas com momento linear p. O coeficiente inicial 2 é a dupla degeneração de spin dos férmions. A primeira fração é o volume do espaço de fases em um diferencial de momentos dividido pelo volume de uma determinada seção no espaço. A h³ é a constante de Planck ao cubo que, como se tem dito, significa o volume dessas seções nas quais cabem até duas partículas com spins opostos. O último termo fracionário é o denominado fator de preenchimento. K é a constante de Boltzmann, T a temperatura, E_p a energia cinética de uma partícula com momento p e ψ o parâmetro de degeneração, que é dependente da densidade e da temperatura.

• O fator de preenchimento indica a probabilidade de este preencher um estado. Seu valor está compreendido entre 0 (todos vazios) e 1 (todos preenchidos).

• O parâmetro de degeneração indica o grau de degeneração das partículas. Se toma valores grandes e negativos a matéria estará em um regime de gás ideal. Se está próximo a 0 a degeneração se começa a notar. Diz-se que o material está parcialmente degenerado. Se o valor é grande e positivo o material está altamente degenerado. Isto acontece quando as densidades são elevadas ou também quando as temperaturas são baixas.

Desta equação se podem deduzir as integrais do número de partículas, a pressão que exercem e a energia que têm. Estas integrais são possíveis de serem resolvidas analiticamente quando a degeneração é completa.

${\displaystyle n=\int _{0}^{\infty }n(p)dp\qquad P={\frac {1}{3}}\int _{0}^{\infty }n(p)v_{p}pdp\qquad U=\int _{0}^{\infty }E_{p}n(p)dp}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O valor da energia das partículas dependerá da velocidade das partículas, a qual decidirá se se tem-se um gás relativista ou não. No primeiro caso se usarão as equações de Einstein e no segundo valerá a aproximação clássica. Como se pode ver, as relações energia-pressão variam significativamente, sendo maiores as pressões obtidas com a degeneração completa não relativista. É lógico, já que a matéria relativista é mais quente.

• Matéria degenerada não relativista (NR): ${\displaystyle v<\!<c\qquad p=m_{e}v\qquad E_{p}={\frac {p^{2}}{2m_{e}}}\qquad U={\frac {3}{2}}P}$
• ///

  sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

  Matéria degenerada extremamente relativista (ER): ${\displaystyle v\simeq c\qquad p\simeq m_{e}c\qquad E_{p}\simeq pc\qquad U=3P}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

As estrelas típicas com degeneração são as anãs brancas e as anãs marrons sustentadas por elétrons e as estrelas de nêutrons sustentadas por nêutrons degenerados. Considera-se que sua temperatura tende a 0, já que não possuem fonte de calor alguma. Suporemos estes corpos com um parâmetro de degeneração tendente a +infinito.

Um diagrama de fase típico mostrando o ponto crítico.

Em física, termodinâmica, química, físico-química e física da matéria condensada, um ponto crítico, também chamado de estado crítico, ocorre sob condições (tais como valores específicos de temperatura, pressão ou composição) no qual não existem limites de fase. Existem vários tipos de pontos críticos, incluindo pontos críticos líquido-vapor e líquido-líquido.^[1][2]

Índice

• 1Substâncias puras: ponto crítico líquido-vapor
  • 1.1Definição matemática
  • 1.2História
  • 1.3Misturas: ponto crítico líquido-líquido
  • 1.4Definição matemática
• 2Ver também
• 3Referências

Substâncias puras: ponto crítico líquido-vapor

O "ponto crítico" é por vezes usado para denotar o ponto especificamente vapor-líquido crítico de um material, a partir do qual a distinção entre fase a líquida e gasosa não existe.

O ponto crítico de vapor-líquido em um diagrama de fases pressão-temperatura está no extremo de alta temperatura do limite de fase líquido-gás. A linha pontilhada verde mostra o comportamento anômalo da água.^[3]

Como se mostra no diagrama de fases para a direita, isto é o ponto em que a fronteira entre a fase líquida e gasosa termina. Em água, o ponto crítico ocorre em cerca de 647 K. (374 ° C; 705 ° F) e 22,064 MPa (218 atm)

À medida que a substância se aproxima da temperatura crítica, as propriedades da sua fases gasosa e líquida convergem, resultando em apenas uma fase no ponto crítico: um fluido supercrítico homogêneo. O calor de vaporização é zero no ponto crítico e para além dele, por isso não existe distinção entre as duas fases. No diagrama de Pressão-temperatura, o ponto em que a temperatura crítica e pressão crítica satisfazer é chamado de ponto crítico da substância. Acima da temperatura crítica, um líquido não pode ser formada por um aumento da pressão, apesar de um sólido poder ser formado sob uma pressão suficiente. A pressão crítica é a pressão de vapor, à temperatura crítica. O volume crítico é o volume molar de uma mole do material a uma temperatura e pressão críticas.

Propriedades críticas variam de material para material, e para muitas substâncias puras estão prontamente disponíveis na literatura. No entanto, a obtenção de propriedades críticas para misturas é mais desafiador.

Definição matemática

No caso das substâncias puras, há um ponto de inflexão na curva isotérmica crítica (linha de temperatura constante) com um diagrama de Pressão-Volume. Isto significa que, no ponto crítico: ^[4][5][6]

${\displaystyle \left({\frac {\partial p}{\partial V}}\right)_{T}=\left({\frac {\partial ^{2}p}{\partial V^{2}}}\right)_{T}=0}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Isto é, as primeira e segunda derivadas parciais da pressão p no que diz respeito ao volume V são ambos zero, com as derivadas parciais avaliados em temperatura constante T. Esta relação pode ser usada para avaliar dois parâmetros de uma equação de estado em termos das propriedades críticas, tais como os parâmetros a e b na equação de van der Waals.^[4]

Às vezes um conjunto de propriedades reduzidas é definida em termos das propriedades importantes, isto é:^[7]

${\displaystyle T_{r}=T/T_{c}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle p_{r}=p/p_{c}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle V_{r}={\frac {V}{RT_{c}/p_{c}}}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle T_{c}=8a/27Rb,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle V_{c}=3b\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle P_{c}=a/27b^{2},}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle T_{r}}$ é a temperatura reduzida, ${\displaystyle p_{r}}$ é a pressão reduzida, ${\displaystyle V_{r}}$ é a redução do volume, e ${\displaystyle R}$ é a constante universal dos gases.

História

A existência de um ponto crítico foi descoberto pela primeira vez por Charles Cagniard de la Tour em 1822^[8] [9] e nomeado por Thomas Andrews, em 1869.^[10] Ele mostrou que o CO2 poderia ser liquefeito a 31 ° C a uma pressão de 73 atm, mas não a uma temperatura ligeiramente mais elevada, mesmo sob uma pressão muito mais elevada (até 3,000 atm).

A equação de Van der Waals é uma equação de estado de um fluido composto de partículas com um tamanho não desprezável e com forças intermoleculares, como as forças de Van der Waals. A equação, cuja origem remonta a 1873, deve seu nome à Johannes Diderik van der Waals, que recebeu o Prêmio Nobel de Física em 1910 por seu trabalho na equação de estado dos gases e líquidos. Essa equação está baseada na modificação da lei dos gases ideais para que se aproxime da maneira mais precisa do comportamento dos gases reais, tendo em conta seu tamanho diferente de zero e a atração entre suas partículas.

Índice

• 1A energia das moléculas
  • 1.1Fator de compressibilidade
  • 1.2A equação
  • 1.3Propriedades críticas
• 2Referências
• 3Bibliografia
• 4Ver também

A energia das moléculas

${\displaystyle PV=nRT}$ funciona perfeitamente com pressões abaixo de 1 atm e temperaturas muito acima das temperaturas de condensação de um gás (esse é o conceito de gás ideal), uma vez que a pressão baixa (menos partículas por m³) reduz a probabilidade de colisões entre as moléculas e a alta temperatura aumenta a velocidade das moléculas, ou seja, diminui as interações intermoleculares, de modo que uma molécula com alta velocidade e, consequentemente, elevada energia cinética, passe do lado de uma outra molécula sem sofrer desvios consideráveis ou atrações maiores.

Se a molécula apresentasse baixa velocidade, ela seria atraída pela outra molécula e o gás , dependendo das pressões e da energia das moléculas, poderia liquefazer-se. Tal qual um foguete que ao passar perto de um planeta, com baixa velocidade, é atraído pelo campo gravitacional do mesmo, sofrendo um desvio em sua órbita.

Se a molécula for bem rápida, ela consegue escapar da força de atração das outra moléculas proporcionalmente à quantidade de energia que ela detém.

Fator de compressibilidade

Fator de compressibilidade em função da pressão

Há uma grandeza chamada fator de compressibilidade (z) que podemos expressar por: ${\displaystyle z={\frac {PV}{nRT}}}$.

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Para os gases ideais, z deve ser igual a 1 sob qualquer condição de temperatura, volume e/ou pressão. Porém foi observado experimentalmente que z desvia-se consideravelmente de 1 sob pressões mais altas e temperaturas mais baixas, como é mostrado no gráfico.

A equação

Observando isto, Van der Waals formulou sua equação, em 1873, a partir de dados obtidos experimentalmente, ou seja, a equação de Van der Waals é uma equação de estado empírica, e pode ser representada por:

${\displaystyle \left(P+{\frac {n^{2}a}{V^{2}}}\right)\left(V-nb\right)=nRT}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde a e b são constantes empíricas e variam para cada tipo de gás.

A constante a está relacionada com as forças de atração intermoleculares e a constante b está relacionada com o volume molecular. A tabela abaixo nos traz os valores de a e b para alguns gases:

Constantes de van der Waals

Gás	a (litro2•atm/mol2)	b (litro/mol)
H2	0,2444	0,02661
He	0,03412	0,02370
N2	1,390	0,03913
O2	1,360	0,03183
CO	1,485	0,03985
NO	1,340	0,02789
CO2	3,592	0,04267
H2O	5,464	0,03049

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Analisando mais a fundo a equação, nota-se que se o volume for suficientemente grande para a pressão ser baixa, o termo ${\displaystyle {\frac {n^{2}a}{V^{2}}}}$ tornar-se-á muito pequeno, e a soma ${\displaystyle P+{\frac {n^{2}a}{V^{2}}}}$ será praticamente igual a P. Sendo assim, ainda com V muito grande, o termo ${\displaystyle V-nb}$ será praticamente igual a V. Portanto quando a pressão é baixa, essa equação pode ser aproximada para ${\displaystyle PV=nRT}$, 

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Propriedades críticas

Para substâncias puras, a taxa de variação parcial da pressão em relação ao volume é constante no ponto crítico. Além disso, existe um ponto de inflexão na isotérmica crítica (linha de temperatura constante) no diagrama pV. Isso significa que no ponto crítico:

${\displaystyle \left({\frac {\partial p}{\partial V}}\right)_{T}=\left({\frac {\partial ^{2}p}{\partial V^{2}}}\right)_{T}=0}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ou seja, a primeira e a segunda derivada parcial da pressão p em relação ao volume V são ambas zero, com a derivada parcial avaliada sobre temperatura constante T. Essa relação pode ser usada para avaliar dois parâmetros para uma equação de estado em termos das propriedades do ponto crítico.

Em alguns casos, um conjunto de propriedades reduzidas é definido em termos das propriedades críticas, i.e.:^[1]

${\displaystyle T_{r}=T/T_{c}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Transferência física

Finalmente é possível mover calor por transferência física de um objeto quente ou frio de um lugar para outro. Isto é tão simples quanto mover água quente em uma bolsa de água quente e aquecer sua cama ou o movimento de um iceberg e a mudança das correntes oceânicas.

Lei de Newton do resfriamento

Um princípio relacionado, a lei de Newton do resfriamento, estabelece que a taxa de perda de calor de um corpo é proporcional à diferença de temperatura entre o corpo e seus arredores.

A lei é dada pela equação diferencial:

${\displaystyle {\frac {dQ}{dt}}=h\cdot A(T_{\text{env}}-T(t))=-h\cdot A\Delta T(t)\quad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle Q=}$ Energia térmica em joules

${\displaystyle h=}$ Coeficiente de transferência térmica

${\displaystyle A=}$ Área de superfície do calor sendo transferido

${\displaystyle T=}$ Temperatura da superfície do objeto e interior (uma vez que estes são os mesmos nesta aproximação)

${\displaystyle T_{\text{env}}=}$ Temperatura do ambiente

${\displaystyle \Delta T(t)=T(t)-T_{\text{env}}}$ 

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

é o gradiente térmico dependente do tempo entre o ambiente e o objeto

Esta forma de princípio de perda de calor por vezes não é muito precisa; uma formulação precisa pode exigir a análise do fluxo de calor, com base na equação de transferência de calor (transiente) em um meio não homogênea, ou mal condutor. Um análogo para gradientes contínuos é lei de Fourier.

A simplificação seguinte (chamado sistema de análise térmica agrupada e outros termos semelhantes) podem ser aplicados, desde que sejam permitidos pelo número de Biot, que relaciona a condutividade de superfície de condutividade térmica interior de um corpo. Se esta relação permite, isso mostra que o corpo tem relativamente elevada condutividade interna, tais que (em boa aproximação), o corpo inteiro está na mesma temperatura uniforme, mesmo que esta mudança de temperatura como está em resfriamento de fora, pelo meio ambiente. Se este for o caso, dar estas condições o comportamento de decaimento exponencial com o tempo, da temperatura do corpo.

Em tais casos, todo o corpo é tratado como um reservatório de calor em capacitância agrupada, com conteúdo total de calor que é proporcional a simples capacidade de calor total C e T, a temperatura do corpo, ou Q = C T. Da definição de capacidade calorífica C vem a relação C = dq / dt. Diferenciando esta equação com relação ao tempo obtém-se a identidade (válida, desde que as temperaturas no objeto são uniformes em qualquer momento): dQ / dt = C (dT / dt). Esta expressão pode ser usada para substituir dQ / dt na primeira equação, que começa esta seção, acima. Então, se T (t) é a temperatura desse corpo no tempo t , e T_env é a temperatura do ambiente em torno do corpo:

${\displaystyle {\frac {dT(t)}{dt}}=-r(T(t)-T_{\mathrm {env} })=-r\Delta T(t)\quad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde

r = hA/C é a constante positiva característica do sistema. a qual deve estar em unidades de 1/time, e é portanto expressa em termos da constante de tempo característica t₀ dada por: r = 1/t₀ = ΔT/[dT(t)/dt] . Então, em sistemas térmicos, t₀ = C/hA. (A capacidade térmica total C de um sistema pode ser ainda representada pela sua capacidade térmica específica de massa c_p multiplicado por sua massa m, então a constante no tempo t₀ é também dada por mc_p/hA).

Assim, a equação acima também pode ser utilmente escrita:

${\displaystyle {\frac {dT(t)}{dt}}=-{\frac {1}{t_{0}}}\Delta T(t)\quad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A solução de sua equação diferencial, por métodos padrão de integração e substituição de condições de contorno, obtem-se:

${\displaystyle T(t)=T_{\mathrm {env} }+(T(0)-T_{\mathrm {env} })\ e^{-rt}.\quad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Aqui, T(t) é a temperatura no tempo t, e T(0) é a temperatura inicial a tempo zero, ou t = 0.

Se:

${\displaystyle \Delta T(t)\quad }$ é definido como : ${\displaystyle T(t)-T_{\mathrm {env} }\ ,\quad }$ onde ${\displaystyle \Delta T(0)\quad }$ é a temperatura inicial no tempo 0, então a solução Newtoniana é escrita como:

${\displaystyle \Delta T(t)=\Delta T(0)\ e^{-rt}=\Delta T(0)\ e^{-t/t_{0}}.\quad }$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Usos: Por exemplo, modelos climáticos simplificados podem usar resfriamento Newtoniano em vez de uma completa (e computacionalmente cara) código de radiação para manter a temperatura atmosférica.

Uma aplicação dimensional, utilizando circuitos termais

Um conceito muito útil usado em aplicações de transferência de calor é a representação de transferência térmica pelo que é conhecido como circuitos termais. Um circuito termal é a representação da resistência ao fluxo de calor como se fosse um resistor elétrico. A transferência de calor é análogo ao atual e a resistência térmica é análoga à resistência elétrica. O valor da resistência térmica para os diferentes modos de transferência de calor são calculados como os denominadores das equações desenvolvidas. As resistências térmicas dos diferentes modos de transferência de calor são utilizados em análise os modos combinados de transferência de calor. As equações que descrevem os três modos de transferência de calor e suas resistências térmicas, como discutido anteriormente estão resumidos na tabela abaixo:

Equações para modos diferentes de transferência de calor e suas resistências térmicas.

Modo de Transferência	Taxa de Transferência de Calor	Resistência Térmica
Condução	${\displaystyle {\dot {Q}}={\frac {T_{1}-T_{2}}{\frac {L}{kA}}}}$	${\displaystyle {\frac {L}{kA}}}$
Convecção	${\displaystyle {\dot {Q}}={\frac {T_{surf}-T_{envr}}{\frac {1}{h_{conv}A_{surf}}}}}$	${\displaystyle {\frac {1}{h_{conv}A_{surf}}}}$
Radiação	${\displaystyle {\dot {Q}}={\frac {T_{surf}-T_{surr}}{\frac {1}{h_{r}A_{surf}}}}}$	${\displaystyle {\frac {1}{h_{r}A}}}$ ${\displaystyle h_{r}=a\sigma A_{surf}(T_{surf}+T_{surr})(T_{surf}^{2}+T_{surr}^{2})}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Em casos onde existe transferência de calor através de diferentes meios (por exemplo através de um compósito), a resistência equivalente é a soma das resistências dos componentes que compõe o compósito. Igualmente, em casos onde há diferentes modos de transferência de calor, a resistência total é a soma das resistências dos diferentes modos. Usando o conceito do circuito térmico, a quantidade de calor transferido através de qualquer meio é o quociente da mudança de temperatura e a resistência térmica total do meio.

Como exemplo, considerando-se uma parede composta de área de seção transversal A. A composição é feita de uma reboco de cimento de comprimento L₁ com um coeficiente térmico k₁ e papel faceado com fibra de vidro de medida L₂, com coeficiente térmico k₂. A superfície esquerda da parede está em T_i e exposta ao ar com um coeficiente convectivo h_i. O superfície direita da parede está em T_o e exposta ao ar com coeficiente de convecção h_o.

Usando-se o conceito de resistência térmica de fluxo de calor através da composição tem-se o seguinte:

${\displaystyle {\dot {Q}}={\frac {T_{i}-T_{o}}{R_{i}+R_{1}+R_{2}+R_{o}}}={\frac {T_{i}-T_{1}}{R_{i}}}={\frac {T_{i}-T_{2}}{R_{i}+R_{1}}}={\frac {T_{i}-T_{3}}{R_{i}+R_{1}+R_{2}}}={\frac {T_{1}-T_{2}}{R_{1}}}={\frac {T_{3}-T_{o}}{R_{0}}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde

${\displaystyle R_{i}={\frac {1}{h_{i}A}},R_{o}={\frac {1}{h_{o}A}},R_{1}={\frac {L_{1}}{k_{1}A}},R_{2}={\frac {L_{2}}{k_{2}A}}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Barreiras de isolamento e radiação

Ver artigo principal: Isolamento térmico

Isolantes térmicos são materiais especialmente projetados para reduzir o fluxo de calor por limitar a condução, convecção, ou ambos. Barreiras radiantes são materiais os quais refletem radiação e consequentemente reduzem o fluxo de calor das fontes radioativas. Bons isolantes não são necessariamente boas barreiras radiantes, e vice versa. Metal, por exemplo, é um excelente refletor e um isolante pobre exatamente por ser um excelente condutor de calor.

A eficácia de um isolador é indicado pelo seu valor R (resistência). O valor R de um material é o inverso do coeficiente de condução (k) multiplicado pela espessura (d) do isolante. As unidades do valor de resistência são em unidades SI: (K·m²/W)

${\displaystyle {R}={d \over k}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle {C}={Q \over m\Delta T}}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Fibra de vidro rígida, um material de isolamento comum, em um valor R de 4 por polegada (o equivalente a aproximadamente 1,57 por cm, ou 157,5 por metro), o poliestireno expandido alcança um R de 4 por polegada, e o extrudado alcança um R de 5, enquanto concreto moldado, um isolante pobre, tem um valor R de 0,08 por polegada (0,03 por cm, ou 3,15 por metro).^{[6][7][8][9][10]}

A eficácia de uma barreira radiante é indicada pela sua refletividade, que é a fração de radiação refletida. Um material com alta refletividade (em um determinado comprimento de onda) tem um baixo nível de emissões (naquele mesmo comprimento de onda), e vice-versa (em qualquer comprimento de onda específico, refletividade = 1 - emissividade). Uma barreira radiante ideal teria uma refletividade de um e, portanto, refletiria 100% da radiação recebida. Garrafas de vácuo (frascos de Dewar) são "prateados" para esta abordagem. No vácuo do espaço, os satélites usam isolamento multicamada que consiste de muitas camadas de mylar ( um tipo de filme de poliéster aluminizado (pretendendo ser "espelhado") para reduzir significativamente a transferência de calor por radiação e controlar a temperatura dos satélites.^[11]

${\displaystyle p_{r}=p/p_{c}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

${\displaystyle V_{r}={\frac {V}{RT_{c}/p_{c}}}\,}$

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle T_{r}}$ é a temperatura reduzida, ${\displaystyle p_{r}}$ é a pressão reduzida, ${\displaystyle V_{r}}$ é o volume reduzido, e ${\displaystyle R}$ é a constante universal dos gases.

///

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou seja, o comportamento do gás será semelhante ao de um gás ideal.